Question

Advertising expenses are a significant component of the cost of goods sold. Listed below is a frequency distribution showing the advertising expenditures for 40 manufacturing companies. Estimate the mean, median, and standard deviation of advertising expense.

Advertising Expenditure ($millions) Number of companies

$20 to under $30 9

30 to under 40 13

40 to under 50 21

50 to under 60 18

60 to under 70 14

Total 75

Answer 1

Mean = 47

Median = 47.38

Standard Deviation = 12.73

Step-by-step explanation:

Note: You wrote " 40 manufacturing companies, but the total number of companies you actually listed is 75, definitely you meant 75.

Let y represent the range of advertising expenditure, f represent the number of companies, x represent the midpoint of the range of advertising expenditure.

y f x fx fx²

$20 to under $30 9 25 225 5625

$30 to under $40 13 35 455 15925

$40 to under $50 21 45 945 42525

$50 to under $60 18 55 990 54450

$60 to under $70 14 65 910 59150

n = 75
`\sum fx = 3525`

`\sum fx^2 = 177675`

Mean,
`\bar{X} = (\sum fx)/(n)`

`\bar{X} = (3525)/(75) \\\bar{X} = 47`

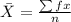
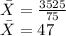
Standard Deviation:

`SD = \sqrt{(n \sum fx^2 - (\sum fx)^2)/(n(n-1)) } \\SD = \sqrt{((75*177675) - (3525)^2)/(75(75-1)) }\\SD = 12.73`

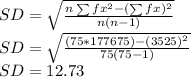
Median:

Get the cumulative frequencies(cf)

y f cf

$20 to under $30 9 9

$30 to under $40 13 22

$40 to under $50 21 43

$50 to under $60 18 61

$60 to under $70 14 75

N = 75

Median = Size of (N/2)th item

Median = Size of (75/2)th item

Median = Size of (37.5)th item

The median class = 40 to under 50

Lower limit, L₁ = 40

Cumulative frequency, cf = 22

f = 21

Class Width, h = 10

Median =
`L_1 + ( (N/2) - cf)/(f) * h\\`

Median =
`40 + ( (75/2) - 22)/(21) * 10\\`

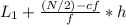
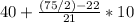
Median = 47.38