Answer:
The number of possible combinations of sports and instrument that Anja can select is 12.
Explanation:
In mathematics, the procedure to select k items from n distinct items, without replacement, is known as combinations.
The formula to compute the combinations of k items from n is given by the formula:
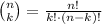
It is said that Anja can choose one sport to play and one instrument to learn using the list below:
Sports: softball, basketball, tennis, or swimming
Instruments: guitar, piano, or clarinet.
There 4 options for sports and 3 for an instrument.
Compute the number of ways to select one sport to play as follows:
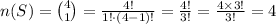
Compute the number of ways to select one instrument to learn as follows:

Compute the number of possible combinations of sports and instrument that Anja can select as follows:
Total number of possible combinations = n (S) × n (I)
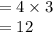
Thus, the number of possible combinations of sports and instrument that Anja can select is 12.