Answer:
a) The total angle of the grinding wheel is 569.88 radians, b) The grinding wheel stop at t = 12.354 seconds, c) The deceleration experimented by the grinding wheel was 8.780 radians per square second.
Step-by-step explanation:
Since the grinding wheel accelerates and decelerates at constant rate, motion can be represented by the following kinematic equations:

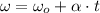

Where:
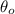 ,
,
 - Initial and final angular position, measured in radians.
- Initial and final angular position, measured in radians.
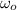 ,
,
 - Initial and final angular speed, measured in radians per second.
- Initial and final angular speed, measured in radians per second.
 - Angular acceleration, measured in radians per square second.
- Angular acceleration, measured in radians per square second.
 - Time, measured in seconds.
- Time, measured in seconds.
Likewise, the grinding wheel experiments two different regimes:
1) The grinding wheel accelerates during 2.40 seconds.
2) The grinding wheel decelerates until rest is reached.
a) The change in angular position during the Acceleration Stage can be obtained of the following expression:
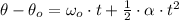
If
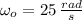 ,
,
 and
and
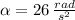 , then:
, then:
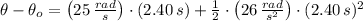
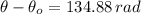
The final angular angular speed can be found by the equation:
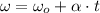
If
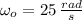 ,
,
 and
and
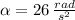 , then:
, then:

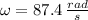
The total angle that grinding wheel did from t = 0 s and the time it stopped is:
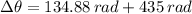
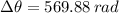
The total angle of the grinding wheel is 569.88 radians.
b) Before finding the instant when the grinding wheel stops, it is needed to find the value of angular deceleration, which can be determined from the following kinematic expression:

The angular acceleration is now cleared:
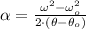
Given that
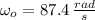 ,
,
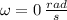 and
and
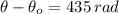 , the angular deceleration is:
, the angular deceleration is:
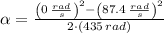
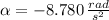
Now, the time interval of the Deceleration Phase is obtained from this formula:
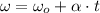
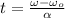
If
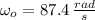 ,
,
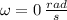 and
and
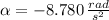 , the time interval is:
, the time interval is:
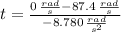
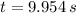
The total time needed for the grinding wheel before stopping is:
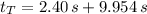
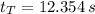
The grinding wheel stop at t = 12.354 seconds.
c) The deceleration experimented by the grinding wheel was 8.780 radians per square second.