Question

I NEEED HELP!!!!! Upon using Thomas Young’s double-slit experiment to obtain measurements, the following data were obtained. Use these data to determine the wavelength of light being used to create the interference pattern.

Do this using three different methods.
The angle to the eighth maximum is 1.12°.
The distance from the slits to the screen is 302.0 cm.
The distance from the central maximum to the fifth minimum is 3.33cm.
The distance between the slits is 0.000250 m

Answer 1

The correct answer is
`6.1*10^(-7)\:m`

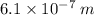
Step-by-step explanation:

The distance from the central maxima to 5th minimum is:

`x_(5n)-x_(0) =3.33\:cm=0.033\:m`

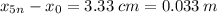
The distance between the slits and the screen:

`L = 302\:cm = 3.02\:m`

Distance between 2 slits:
`d = 0.00025\:m`

`(n-(1)/(2))\lambda=(d(x_n))/(L)`

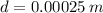
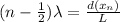
For fifth minima, n = 5... so we have:

`x_(5n)=(9\lambda L)/(2d)`

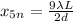
For central maxima, n = 0... so we have:

`x_(0)=(n\lambda L)/(d)=0`

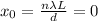
So the distance from central maxima to 5th minimum is:

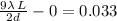`(9\lambda \:L)/(2d)-0=0.033` (Putting the values, we get):

`\Rightarrow \lambda = 6.1* 10^(-7)\:m`

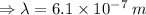
Best Regards!

Answer 2

The wavelength is approximately 611 nm

Step-by-step explanation:

We can use the formula for the condition of maximum of interference given by:

`d\,sin(\theta)=m\,\lambda\\(0.000250\,\,m)\,\,sin(1.12^o)=8\,\lambda\\\lambda=(1)/(8) \,(0.000250\,\,m)\,\,sin(1.12^o)\\\lambda \approx 610.8\,\,nm`

We can also use the formula for the distance from the central maximum to the 5th minimum by first finding the tangent of the angle to that fifth minimum:

`tan(\theta)=(y)/(D)\\ tan(\theta)=(0.0333)/(3.02) =0.011026`

and now using it in the general formula for minimum:

`d\,sin(\theta)\approx d\,tan(\theta)=(m-(1)/(2) )\,\lambda\\\lambda\approx 0.00025\,(0.011026)/(4.5)\,\,m\\\lambda\approx 612.55\,\,nm`