Question

Part A: Explain why the x-coordinates of the points where the graphs of the equations y = 2−x and y = 4x + 3 intersect are the solutions of the equation 2−x = 4x + 3. (4 points) Part B: Make tables to find the solution to 2−x = 4x + 3. Take the integer values of x only between −3 and 3. (4 points) Part C: How can you solve the equation 2−x = 4x + 3 graphically? (2 points) PLez Answer 50 points

Answer 1

Explanation:

Part A:

We have two lines: y = 2 - x and y = 4x + 3 . Given two equations that are both required to be true. The answer is the points where the lines cross, this means we have to make the equations equal to each other. It will look like this:

2 - x = 4x + 3

Part B:

In order to solve the equation we need to put the like terms together. So we will add x on each side.

2 - x = 4x + 3

+x +x

So now we get:

2 = 5x + 3

Now that x is on one side and is positive we will move 3 on the left side by subtracting it from each side.

2 = 5x + 3

-3 -3

So now we get:

-1 = 5x

Now that the like terms have been combined we need to find out what x alone is so we divide 5 on each side:

`(-1)/(5)` =
`(5x)/(5)`

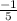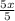
No we see that:

x =
`-(1)/(5)`