Question

Two wires of circular cross section are made of the same metal. Wire 1 has radius rr and length LL; wire 2 has radius 2r2r and length 2L2L. The potential difference between the ends of the wire is the same for both wires. Find the ratio of the resistance of wire 2 to the resistance of wire 1.

Answer 1

Ratio of wire 2 to wire 1 is 0.5 : 1

Step-by-step explanation:

Wire 1:

length = L

radius = r

Wire 2:

length = 2L

radius = 2r

Resistance of a conductor varies directly as the length and inversely as the cross sectional area. Mathematically

`R = (pl)/(a)`

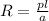
l = length of conductor

a = cross sectional area of the conductor

p = resistivity of the material with which the conductor is made.

since we are considering the same material, we can ignore the resistivity of the wire.

For wire 1

cross sectional area =
`\pi r^(2)`

therefore,

resistance R =
`(L)/(\pi r^(2) )`

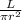
For the second wire 2

cross sectional area =
`4\pi r^(2)`

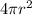
therefore,

resistance R =
`(2L)/(4\pi r^(2) )`

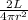
Ratio of wire 2 to wire 1 will be

`(2L)/(4\pi r^(2) )` ÷
`(L)/(\pi r^(2) )` =
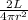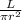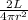`(2L)/(4\pi r^(2) )` x
`(\pi r^(2) )/(L)`

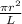
Ratio of resistance of wire 2 to wire 1 = 2/4 = 0.5 : 1