Question

Consider a circle whose equation is x2 + y2 + 4x – 6y – 36 = 0. Which statements are true? Check all that apply. To begin converting the equation to standard form, subtract 36 from both sides. To complete the square for the x terms, add 4 to both sides. The center of the circle is at (–2, 3). The center of the circle is at (4, –6). The radius of the circle is 6 units. The radius of the circle is 49 units.

Answer 1

the answers are 2 and 3

Explanation:

Answer 2

1) False, to begin converting the equation to standard form, each side must be added by 36. 2) True, to complete the square for the x terms, add 4 to both sides, 3) True, the center of the circle is at (-2, 3), 4) False, the center of the circle is at (-2, 3), 5) False, the radius of the circle is 7 units, 6) False, the radius of the circle is 7 units.

Explanation:

Let prove the validity of each choice:

1) To begin converting the equation to standard form, subtract 36 from both sides:

Let consider the following formula and perform the following algebraic operations:

(i)
`x^(2) + y^(2) + 4\cdot x - 6\cdot y - 36 = 0` Given

(ii)
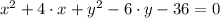`x^(2) + 4\cdot x + y^(2) - 6\cdot y - 36 = 0` Commutative Property

(iii)
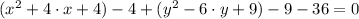`(x^(2) + 4\cdot x + 4) - 4 + (y^(2) - 6\cdot y + 9) - 9 -36 = 0` Modulative/Associative Property/Additive Inverse Existence

(iv)
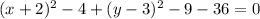`(x+ 2)^(2) - 4 + (y - 3)^(2) - 9 - 36 = 0` Perfect Trinomial Square

(v)
`(x+2)^(2) +(y-3)^(2) = 4 + 9 + 36` Commutative Property/Compatibility with Addition/Additive Inverse Existence/Modulative Property

(vi)
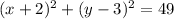`(x+2)^(2) + (y-3)^(2) = 49` Definition of Addition/Result

False, to begin converting the equation to standard form, each side must be added by 36.

2) True, step (iii) on exercise 1) indicates that both side must be added by 4.

3) The general equation for a circle centered at (h, k) is of the form:

`(x-h)^(2)+ (y-k)^(2) = r^(2)`

Where
`r` is the radius of the circle.

By direct comparison, it is evident that circle is centered at (-2,3).

True, step (vi) on exercise 1) indicates that center of the circle is at (-2, 3).

4) False, step (vi) on exercise 1) indicates that the center of the circle is at (-2, 3), not in (4, -6).

5) After comparing both formulas, it is evident that radius of the circle is 7 units.

False, the radius of the circle is 7 units.

6) After comparing both formulas, it is evident that radius of the circle is 7 units.

False, the radius of the circle is 7 units.