Question

An experiment consists of dealing 7 cards from a standard deck of 52 playing cards. What is the probability of being dealt exactly 4 clubs and 3 spades?

Answer 1

Answer: 0.00153

Explanation:

Given: An experiment consists of dealing 7 cards from a standard deck of 52 playing cards.

Number of ways of dealing 7 cards from 52 cards =
`^(52)C_7`

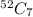
Since there are 13 clubs and 13 spades.

Number of ways of getting exactly 4 clubs and 3 spades=
`^(13)C_4*\ ^(13)C_3`

Now, the probability of being dealt exactly 4 clubs and 3 spades

`=(^(13)C_4*\ ^(13)C_3)/(^(52)C_7)\\\\\\=\frac{{(13!)/(4!(9!))*(13!)/(3!10!)}}{(52!)/(7!45!)}\\\\=(715*286)/(133784560)\\\\=0.00152850224271\approx0.00153`

Hence, the probability of being dealt exactly 4 clubs and 3 spades = 0.00153