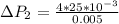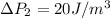Question

Consider two soap bubbles with radius r1 and r2 (r1 <r2) connected via a valve. What happens if we open the valve​

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

The pressure difference of the first bubble is
`\Delta P _1 =10 J/m^3`

The pressure difference of the second bubble is
`\Delta P _2 =20 J/m^3`

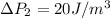
The pressure difference on the second bubble is higher than that of the first bubble so when the valve is opened pressure from second bubble will cause air to flow toward the first bubble making is bigger

Step-by-step explanation:

From the question we are told that

The radius of the first bubble is
`r_1 = 10 \ mm=0.01 \ m`

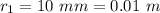
The radius of the second bubble is
`r_2 = 5 \ mm = 0.005 \ m`

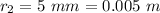
The surface tension of the soap solution is
`s = 25 \ mJ/m^2 = 25*10^(-3) J/m^2`

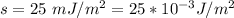
Generally according to the Laplace's Law for a spherical membrane the pressure difference is mathematically represented as

`\Delta P = (4 s)/(R)`

Now the pressure difference for the first bubble is mathematically evaluated as

`\Delta P _1 = (4 s)/(r_1)`

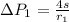
substituting values

`\Delta P _1 = (4 *25 *10^(-3))/(0.01)`

`\Delta P _1 =10 J/m^3`

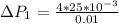
Now the pressure difference for the second bubble is mathematically evaluated as

`\Delta P _2 = (4 s)/(r_1)`

`\Delta P _2 = (4 *25 *10^(-3))/(0.005)`

`\Delta P _2 =20 J/m^3`