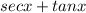Prove the identity cos x/1 - sin x = sec x + tan x

Question

asked Nov 28, 2021 24.0k views

1 Answer

Nate Weiner · Answer 1 · 2021-12-04T04:39:55+0000

Answer:

Proved

Explanation:

Given

Prove that

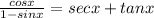
(cos x)/(1 - sin x) = sec x + tan x

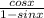
(cos x)/(1 - sin x)

Multiply the numerator and denominator by 1 + sinx

(cos x)/(1 - sin x) * (1 + sin x)/(1 + sin x)

Combine both fractions to form 1

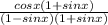
(cos x (1 + sin x))/((1 - sin x)(1 + sin x))

Expand the denominator using difference of two squares;

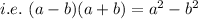
$i.e.\ (a - b)(a + b) = a^2 - b^2$

The expression becomes

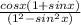
(cos x (1 + sin x))/((1^2 - sin^2 x))

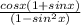
(cos x (1 + sin x))/((1 - sin^2 x))

From trigonometry;
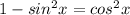
1 - sin^2x = cos^2x

The expression becomes

(cos x (1 + sin x))/((cos^2 x))

Divide the numerator and the denominator by cos x

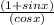
((1 + sin x))/((cos x))

Split fraction

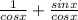
(1)/(cos x) + (sin x)/(cos x)

From trigonometry;
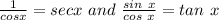
$(1)/(cos x) = sec x \ and\ (sin\ x)/(cos\ x) = tan\ x$

So;

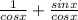(1)/(cos x) + (sin x)/(cos x) =
sec x + tan x