Question

PLEASE. NEED HELP. Find the sum.

Answer 1

Distribute the sum:

`\displaystyle\sum_(i=1)^(24)(3i-2)=3\sum_(i=1)^(24)i-2\sum_(i=1)^(24)1`

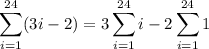
Use the following formulas:

`\displaystyle\sum_(i=1)^n1=n`

`\displaystyle\sum_(i=1)^ni=\frac{n(n+1)}2`

`\implies\displaystyle\sum_(i=1)^(24)(3i-2)=3\cdot\frac{24\cdot25}2-2\cdot24=\boxed{852}`

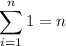
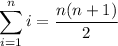
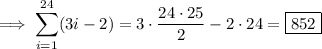
In case you don't know where those formulas came from:

The first one is obvious; you're just adding n copies of 1, so 1 + 1 + ... + 1 = n.

The second can be proved in this way: let S be the sum 1 + 2 + 3 + ... + n. Rearrange it as S = n + (n - 1) + (n - 2) + ... + 1. Then 2S = (n + 1) + (n + 1) + (n + 1) + ... + (n + 1), or n copies of n + 1. So 2S = n(n + 1). Divide both sides by 2 and we're done.