Question

A physicist is designing a cyclotron to accelerate protons to one-tenth the speed of light. The magnetic field will have a strength of 1.6 T. (a) Determine the rotational period (in s) of the circulating protons. s (b) Determine the maximum radius (in m) of the protons' orbit

Answer 1

(a) T = 4.09*10^-8 s

(b) r = 0.19m

Step-by-step explanation:

(a) In order to determine the rotational period of the protons, you first calculate the angular speed of the proton. You use the following formula for the radius of the trajectory described by the electron in a region with a constant magnetic field:

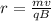`r=(mv)/(qB)` (1)

m: mass of the proton = 1.67*10^-27 kg

q: charge of the proton = 1.6*10⁻19C

B: magnitude of the magnetic field = 1.6T

v: speed of the proton = 0.1c = 0.1(3*10^8m/s) = 3*10^7m/s

The angular speed of the proton is v/r, then, you solve for w in the equation (1) and replace the values of the parameters:

`\omega=(v)/(r)=(qB)/(m)\\\\\omega=((1.6*10^(-19)C)(1.6T))/(1.67*10^(-27)kg)=1.53*10^8(rad)/(s)`

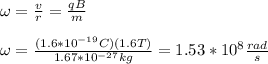
The rotational period T is:

`T=(2\pi)/(1.53*10^8rad/s)=4.09*10^(-8)s`

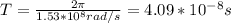
(b) The radius of the protons' orbit is calculated by using the equation (1):

`r=((1.67*10^(-27)kg)(3*10^7m/s))/((1.6*10^(-19)C)(1.6T))\\\\r=0.19m`

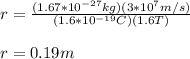
The radius of the protons' orbit is 0.19m