Question

Near the surface of Earth, an electric field points radially downward and has a magnitude of approximately 100 N/C. What charge (magnitude and sign) would have to be placed on a penny that has a mass of 3 g to cause it to rise into the air with an upward acceleration of 0.19 m/s2?

Answer 1

q = 2.997*10^-4C

Step-by-step explanation:

In order to find the required charge that the penny have to have, to acquire an upward acceleration, you take into account that the electric force on the penny must be higher than the weight of the penny.

You use the second Newton law to sum both electrical and gravitational forces:

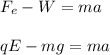`F_e-W=ma\\\\qE-mg=ma` (1)

Fe: electric force

W: weight of the penny

q: required charge = ?

m: mass of the penny = 3g = 0.003kg

E: magnitude of the electric field = 100N/C

g: gravitational acceleration = 9.8m/s^2

a: acceleration of the penny = 0.19m/s^2

You solve the equation (1) for q, and replace the values of the other parameters:

`q=(ma+mg)/(E)=(m(a+g))/(E)\\\\q=((0.003kg)(0.19m/s^2+9.8m/s^2))/(100N/C)\\\\q=2.997*10^(-4)C`

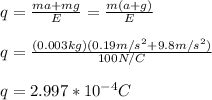
It is necessary that the penny has a charge of 2.997*10^-4 C, in order to acquire an upward acceleration of 0.19m/s^2