Question

Solve the logarithmic equation. Show steps

Answer 1

`\begin{array}{llll} \textit{Logarithm of rationals} \\\\ \log_a\left( (x)/(y)\right)\implies \log_a(x)-\log_a(y) \end{array}~\hfill \begin{array}{llll} \textit{Logarithm Cancellation Rules} \\\\ log_a a^x = x\qquad \qquad \underset{\stackrel{\uparrow }{\textit{let's use this one}}}{a^(log_a x)=x} \end{array} \\\\[-0.35em] ~\dotfill`

`\log_4(x+10)-\log_4(x-2)=\log_4(x)\implies \log_4\left( \cfrac{x+10}{x-2} \right)=\log_4(x) \\\\\\ \stackrel{\textit{exponentializing both sides}}{4^{\log_4\left( (x+10)/(x-2) \right)}=4^(\log_4(x))}\implies \cfrac{x+10}{x-2}=x\implies x+10=x^2-2x \\\\\\ 10=x^2-3x\implies 0=x^2-3x-10 \\\\\\ 0=(x-5)(x+2)\implies x= \begin{cases} 5~~\checkmark\\ -2 \end{cases}`

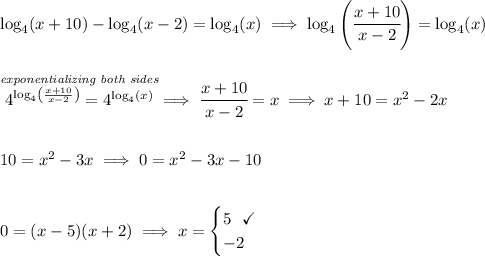
notice, -2 is a valid value for the quadratic, however, the argument value for a logarithm can never 0 or less, it has to be always greater than 0, so for the logarithmic expression with (x-2), using x = -2 will give us a negative value, so -2 is no dice.