Answer:
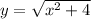
Explanation:
The question is incomplete. Here is the complete question.
Find the solution of the differential equation that satisfies the given initial condition. dy/dx = x/y, y(0) = -2
Using the variable separable method.
Step 1: Separate the variables
dy/dx = x/y
x dx = y dy
Step 2: Integrate both sides of the resulting equation
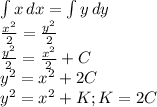
Note that the constant of integration added to the side containing x
Step 3: Apply the initial condition y(0) = -2
This means when x = 0, y = -2. From step 2:
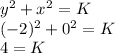
Step 4: Substitute K = 4 into the resulting differential equation above
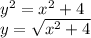
This gives the solution to the differential equation.