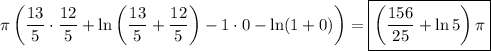Question

Find the area of the surface generated by revolving the curve xequalsStartFraction e Superscript y Baseline plus e Superscript negative y Over 2 EndFraction in the interval 0 less than or equals y less than or equals ln 5 about the​ y-axis.

Answer 1

The area is given by the integral,

`\displaystyle\int_0^(\ln5)2\pi x(y)\sqrt{1+\left((\mathrm dx)/(\mathrm dy)\right)^2}\,\mathrm dy`

We have

`x=\frac{e^y+e^(-y)}2\implies(\mathrm dx)/(\mathrm dy)=\frac{e^y-e^(-y)}2`

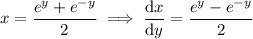
So now compute the integral:

`\displaystyle\frac\pi2\int_0^(\ln5)(e^y+e^(-y))\sqrt{4+(e^y-e^(-y))^2}\,\mathrm dy`

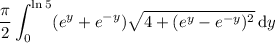
Substitute
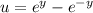`u=e^y-e^(-y)` and
`\mathrm du=(e^y+e^(-y))\,\mathrm dy`:

`\displaystyle\frac\pi2\int_0^{\frac{24}5}√(4+u^2)\,\mathrm du`

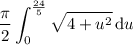
Another substitution,
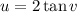`u=2\tan v` and
`\mathrm dv=2\sec^2v\,\mathrm dv`:

`\displaystyle\frac\pi2\int_0^{\tan^(-1)\frac{12}5}√(4+(2\tan v)^2)\,2\sec^2v\,\mathrm dv`

`\displaystyle2\pi\int_0^{\tan^(-1)\frac{12}5}√(1+\tan^2v)\,\sec^2v\,\mathrm dv`

`\displaystyle2\pi\int_0^{\tan^(-1)\frac{12}5}\sec^3v\,\mathrm dv`

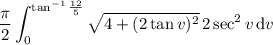
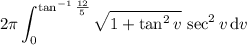
There's a well-known formula for the integral of secant cubed, but if you don't know it off the top of your head (like me), you can integrate by parts:

`\displaystyle I=\int\sec^3v\,\mathrm dv=\sec v\tan v-\int\sec v\tan^2v\,\mathrm dv`

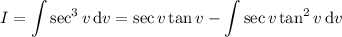
Expand the remaining the integral in terms of powers of secant:

`\displaystyle\int\sec v\tan^2v\,\mathrm dv=\int\sec v(\sec^2v-1)\,\mathrm dv=\int\sec^3v\,\mathrm dv-\int\sec v\,\mathrm dv`

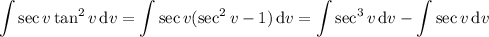
so that

`I=\sec v\tan v-\left(I-\displaystyle\int\sec v\,\mathrm dv\right)`

`2I=\sec v\tan v+\displaystyle\int\sec v\,\mathrm dv`

`\implies I=\displaystyle\int\sec^3v\,\mathrm dv=\frac{\sec v\tan v}2+\frac12\ln|\sec v+\tan v|+C`

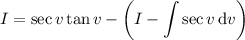
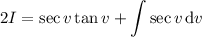
Coming back to the area integral, we use the formula above to get

`\displaystyle2\pi\int_0^{\tan^(-1)\frac{12}5}\sec^3v\,\mathrm dv=\pi\left(\sec v\tan v+\ln|\sec v+\tan v|\right)\bigg|_0^{\tan^(-1)\frac{12}5}`

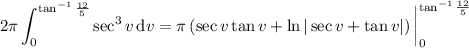
Next,

`\tan\left(\tan^(-1)\frac{12}5\right)=\frac{12}5`

`\sec\left(\tan^(-1)\frac{12}5\right)=\frac{13}5`

`\tan0=0`

`\sec0=1`

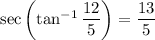
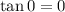
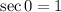
so the area is

`\pi\left(\frac{13}5\cdot\frac{12}5+\ln\left(\frac{13}5+\frac{12}5\right)-1\cdot0-\ln(1+0)\right)=\boxed{\left((156)/(25)+\ln5\right)\pi}`