Question

Hannah notices that segment HI and segment KL are congruent in the image below: Two triangles are shown, GHI and JKL. G is at negative 3, 1. H is at negative 1, 1. I is at negative 2, 3. J is at 3, 3. K is at 1, 3. L is at 2, 1. Angle I and L are shown as congruent. Which step could help her determine if ΔGHI ≅ ΔJKL by SAS? (5 points) segment IG ≅ segment LJ segment GH ≅ segment KL ∠G ≅ ∠ K ∠L ≅ ∠ H

Answer 1

segment IG ≅ segment LJ

Explanation:

Please refer to the attached image as per the triangles as given in the question statement.

`\triangle HGI, \triangle JKL`

`G\left(-3,1\right),\ H\left(-1,1\right),\ I\left(-2,3\right)`

`J\left(3,3\right),K\left(1,3\right),L\left(2,1\right)`

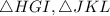
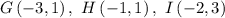
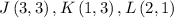
Given that:

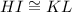`HI\cong KL` and

`\angle I \cong \angle L`

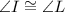
SAS congruence between two triangles states that two triangles are congruent if two corresponding sides and the angle between the two sides are congruent.

We are given that one angle and one sides are congruent in the given triangles.

We need to prove that other sides that makes this angle are also congruent.

To show the triangles are congruent i.e.
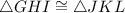`\triangle GHI \cong \triangle JKL` by SAS congruence we need to prove that

segment IG ≅ segment LJ

Let us use Distance formula to find IG and LJ:

`D = √((x_2-x_1)^2+(y_2-y_1)^2)`

`IG =√((-2+3)^2+(3-1)^2) =\sqrt5\ units`

`LJ =√((2-3)^2+(1-3)^2) =\sqrt5\ units`

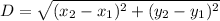
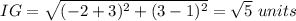
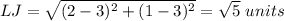
Hence, segment IG ≅ segment LJ

`\therefore` ΔGHI ≅ ΔJKL by SAS