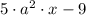Answer:
See explanation below for further details.
Explanation:
A rational consist of two real numbers such that:
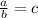
If c is a polynomial with a certain grade, then, both the numerator and the denominator must be also polynomials and the grade of the numerator must be greater than denominator.
If c is linear function, that is, a first order polynomial, then a must be a (n+1)-th polynomial and b must be a n-th polynomial.
Example:
If
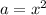 and
and
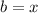 , then:
, then:
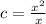

If c is a quadratic function, that is, a second order polynomial, then a must be a (n+1)-th polynomial and b must be a n-th polynomial.
Example
If
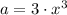 and
and
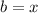 , then:
, then:
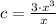

But if c is an exponential, both the numerator and the denominator must be therefore exponential function and grade of each exponential function must different to the other.
Example
If
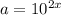 and
and
 , then:
, then:
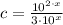
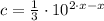
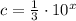
Otherwise, c would be equal to a constant function, that is, a polynomial with a grade 0.
If
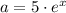 and
and
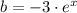 , then:
, then:
Example
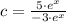

It is worth to add that exponential functions can be a linear combination of single exponential function, similar to polynomials.
Example