Complete Question
Grandpa and Grandma are treating their family to the movies. Matinee tickets cost $4 per child and $4 per adult. Evening tickets cost $6 per child and $8 per adult. They plan on spending no more than $80 on the matinee tickets and no more than $100 on the evening tickets. Could they take 9 children and 4 adults to both shows? Show your work. A yes or no answer is not sufficient for credit.
Answer:
Yes it is possible to take the 9 children and 4 adults to both shows
Explanation:
From the question we are told that
The cost of the Matinee tickets for a child is z = $4
The cost of the Matinee tickets for an adult is a = $ 4
The cost of the Evening tickets for a child is k = $6
The cost of the Evening tickets for an adult is b = $8
The maximum amount to be spent on Matinee tickets is m = $80
The maximum amount to be spent on Evening tickets is e = $100
The number of child to be taken to the movies is n = 9
The number of adults to be taken to the movies is j = 4
Now the total amount of money that would be spent on Matinee tickets is mathematically evaluated as

substituting values
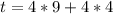
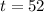
Now the total amount of money that would be spent on Evening ticket is mathematically evaluated as
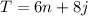
substituting values
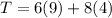
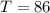
This implies that it is possible to take 9 children and 4 adults to both shows
given that

i.e $56
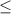 $ 80
$ 80
and

i.e $ 86
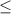 $ 100
$ 100