Question

Eagle Outfitters is a chain of stores specializing in outdoor apparel and camping gear. They are considering a promotion that involves mailing discount coupons to all their credit card customers. This promotion will be considered a success if more than 10% of those receiving the coupons use them. Before going national with the promotion, coupons were sent to a sample of 100 credit card customers.

a. Develop hypotheses that can be used to test whether the population proportion of those
who will use the coupons is sufficient to go national.
b. The file Eagle contains the sample data. Develop a point estimate of the population
proportion.
c. Use αα= .05 to conduct your hypothesis test. Should Eagle go national with the
promotion?

Answer 1

a) Alternative hypothesis: the use of the coupons is isgnificantly higher than 10%.

Null hypothesis: the use of the coupons is not significantly higher than 10%.

The null and alternative hypothesis can be written as:

`H_0: \pi=0.1\\\\H_a:\pi>0.1`

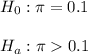
b) Point estimate p=0.13

c) At a significance level of 0.05, there is not enough evidence to support the claim that the proportion of coupons use is significantly higher than 10%.

Eagle should not go national with the promotion as there is no evidence it has been succesful.

Explanation:

The question is incomplete.

The sample data shows that x=13 out of n=100 use the coupons.

This is a hypothesis test for a proportion.

The claim is that the proportion of coupons use is significantly higher than 10%.

Then, the null and alternative hypothesis are:

`H_0: \pi=0.1\\\\H_a:\pi>0.1`

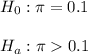
The significance level is 0.05.

The sample has a size n=100.

The point estimate for the population proportion is the sample proportion and has a value of p=0.13.

`p=X/n=13/100=0.13`

The standard error of the proportion is:

`\sigma_p=\sqrt{(\pi(1-\pi))/(n)}=\sqrt{(0.1*0.9)/(100)}\\\\\\ \sigma_p=√(0.0009)=0.03`

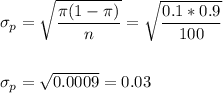
Then, we can calculate the z-statistic as:

`z=(p-\pi-0.5/n)/(\sigma_p)=(0.13-0.1-0.5/100)/(0.03)=(0.025)/(0.03)=0.833`

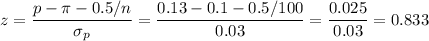
This test is a right-tailed test, so the P-value for this test is calculated as:

`\text{P-value}=P(z>0.833)=0.202`

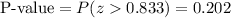
As the P-value (0.202) is greater than the significance level (0.05), the effect is not significant.

The null hypothesis failed to be rejected.

At a significance level of 0.05, there is not enough evidence to support the claim that the proportion of coupons use is significantly higher than 10%.