Question

Un contenedor de 1800 N está en reposo sobre un plano inclinado a 28°, el coeficiente de fricción entre el contenedor y el plano es de 0.4. Calcule la fuerza P paralela al plano y dirigida hacia arriba de éste que hará que el contenedor se mueva hacia arriba con una velocidad constante.

Answer 1

F = 1480.77N

Step-by-step explanation:

In order to calculate the required force to push the container with a constant velocity, you take into account the the sum of force on the container is equal to zero. Furthermore, you have for an incline the following sum of forces:

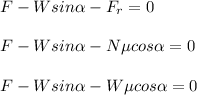`F-Wsin\alpha-F_r=0\\\\F-Wsin\alpha-N\mu cos\alpha=0\\\\F-Wsin\alpha-W\mu cos\alpha=0` (1)

F: required force = ?

W: weight of the container = 1800N

N: normal force = weigth

α: angle of the incline = 28°

g: gravitational acceleration = 9.8m/s^2

μ: coefficient of friction = 0.4

You solve the equation (1) for F and replace the values of the other parameters:

`F=W(sin\alpha+\mu cos\alpha)\\\\F=(1800N)(sin28\°+(0.4)cos28\°)=1480.77N`

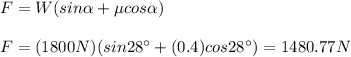
The required force to push the container for the incline with a constant velocity is 1480.77N