Question

If you add 36, 35, 34, 33, and 32, the sum is . If you sum the numbers from 1 to 36, the sum is . The fraction (the first sum / the total sum) to the nearest tenth = %. The lender will multiply this fraction by the total interest. The cumulative interest = (the percentage calculated above) x ($808.13) = $. The difference between the amount paid under a standard amortization plan and the amount paid under a Rule of 78 plan is: $

Answer 1

If you add 36, 35, 34, 33, and 32, the sum is . If you sum the numbers from 1 to 36, the sum is . The fraction (the first sum / the total sum) to the nearest tenth = %. The lender will multiply this fraction by the total interest. The cumulative interest = (the percentage calculated above) x ($808.13) = $. The difference between the amount paid under a standard amortization plan and the amount paid under a Rule of 78 plan is: $

1

SEE ANSWER

ADD ANSWER

Explanation:

Answer 2

Complete Question

Consider a three-year loan (so we'll assume the numbers 1 through 36) for $5,000 with interest at 10% per year. Using standard amortization, the monthly payment is $161.33. In this example, we will not worry about exact or ordinary interest because the total interest to be paid is $808.13. After the fifth month the borrower decides to prepay the whole loan. Under a standard amortization plan the borrower would have paid $198.28 in cumulative interest. However, using the Rule of 78 a lender would calculate the fraction of the total interest based on two series:

`\frac{(n+35)+(n+34)+(n+33)+(n+32)+(n+31)} {(n)+(n+1)+...+(n+35)}`

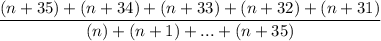
Answer:

See below

Explanation:

36+35+34+33+32=170

• If you add 36, 35, 34, 33, and 32, the sum is 170.

Now, 1,2,3,...36 forms an arithmetic series whose first and last term are 1 and 36 respectively. Its sum is determined using the formula:
`S_(n)=(n)/(2)(a+l) \\`

`S_(36)=(36)/(2)(1+36) =18*37=666`

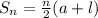
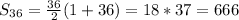
• If you sum the numbers from 1 to 36, the sum is 666.

`=(170)/(666)= 0.255=25.5\% $(to the nearest tenth)`

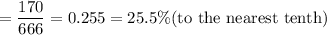
• The fraction (the first sum / the total sum) to the nearest tenth = 25.5%.

The lender will multiply this fraction by the total interest.

• The cumulative interest
  `= 25.5\% * \$808.13 = \$206.07`

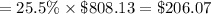
The difference between the amount paid under a standard amortization plan and the amount paid under a Rule of 78 plan is:

$206.07-198.28=$7.79