Question

Objects A and B are both positively charged. Both have a mass of 900 g, but A has twice the charge of B. When A and B are placed 30.0 cm apart, B experiences an electric force of 0.870 N.

How large is the force on A?
What is the charge on qA and qB?
If the objects are released, what is the initial acceleration of A?

Answer 1

- Force on A = 0.870N

- charge of the object B = q = 2.1 μC

charge of the object A = 2q = 4.2 μC

- a = 0.966 m/s^2

Step-by-step explanation:

- In order to determine the force on the object A, you take into account the third Newton law, which states that the force experienced by A has the same magnitude of the force experienced by B, but with an opposite direction.

Then, the force on A is 0.870N

- In order to calculate the charge of both objects, you use the following formula:

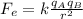`F_e=k(q_Aq_B)/(r^2)` (1)

k: Coulomb's constant = 8.98*10^9 Nm^2/C^2

r: distance between the objects = 30.0cm = 0.30m

A has twice the charge of B. If the charge of B is qB=q, then the charge of A is qA=2qB = 2q.

You replace the expression for qA and qB into the equation (1), solve for q, and replace the values of the parameters.

`F_e=k((2q)(q))/(r^2)=2k(q^2)/(r^2)\\\\q=\sqrt{(r^2Fe)/(2k)}\\\\q=\sqrt{((0.30m)^2(0.870N))/(2(8.98*10^9Nm^2/C^2))}=2.1*10^(-6)C\\\\q=2.1\mu C`

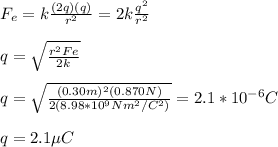
Then, you have:

charge of the object B = q = 2.1 μC

charge of the object A = 2q = 4.2 μC

- In order to calculate the acceleration of A, you use the second Newton law with the electric force, as follow:

`F_e=ma\\\\a=(F_e)/(m)`

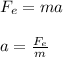
m: mass of the object A = 900g = 0.900kg

`a=(0.870N)/(0.900kg)=0.966(m)/(s^2)`

The acceleration of A is 0.966m/s^2