Question

A soda factory has a special manufacturing line to fill large bottles with 2 liters of their beverage. Every process is computerized. However, it doesn't always fill exactly 2 liters. It follows a normal distribution, witha mean of 1.98 liters and a variance of 0.0064 liters. If the amount of soda in a bottle is more than 1.5 standard deviations away from the mean, then it will be rejected. Find the probability that a randomly selected bottle is rejected.

A 0
B 0.04
C 0.07
D 0.13
E 0.

Answer 1

`z= (2.1-1.98)/(0.08)= 1.5`

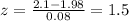
And we can use the normal standard table and the complement rule and we got:

`P(z>1.5)= 1-P(Z<1.5) =1- 0.933= 0.067 \approx 0.07`

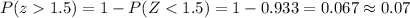
And the best answer would be:

C 0.07

Explanation:

Let X the random variable who represent the amount of soda filled in large bottles and we know this:

`\mu = 1.98, \sigma =√(0.0064)= 0.08`

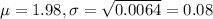
And we want to find this probability:

`P(X> \mu +1.5 \sigma = 1.98 +1.5*0.08 =2.1)`

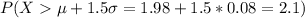
And for this case we can use the z score formula given by:

`z=(X -\mu)/(\sigma)`

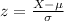
And replacing we got:

`z= (2.1-1.98)/(0.08)= 1.5`

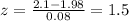
And we can use the normal standard table and the complement rule and we got:

`P(z>1.5)= 1-P(Z<1.5) =1- 0.933= 0.067 \approx 0.07`

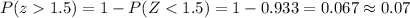
And the best answer would be:

C 0.07