Question

A Carnot engine operates between a high temperature reservoir at 435 K and a river with water at 280 K. If it absorbs 3700 J of heat each cycle, how much work per cycle does it perform?

Answer 1

The work done by the carnot engine per cycle is 1318.31 J

Step-by-step explanation:

Given;

high temperature reservoir, Th = 435 k

temperature of river water, Tl = 280 k

heat energy absorbed per cycle, Q = 3700 J

Determine the work done per cycle is calculated as;

`W = Q(1-(T_l)/(T_h) )`

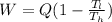
Where;

W is the work done

Q is the absolute heat absorbed per cycle

Tl is the temperature of the cold liquid

Th is the temperature of the hot reservoir

`W = Q(1-(T_l)/(T_h) )\\\\W = 3700(1 - (280)/(435) )\\\\W = 3700 (1-0.6437)\\\\W = 1318.31 \ J`

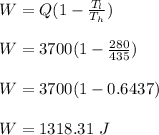
Therefore, the carnot engine operating at the given conditions, performs 1318.31 J work per cycle.