Answer:
The work done lifting the bucket to the top of the building is 341.25 lbf-ft.
Step-by-step explanation:
Given that bucket is part of a variable-mass system due to sand losses and such work, measured in
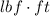 is associated to gravitational potential energy by Work-Energy Theorem, the work done by lifting the bucket is represented by the following integral:
is associated to gravitational potential energy by Work-Energy Theorem, the work done by lifting the bucket is represented by the following integral:
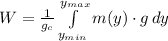
Where:
 - Mass of the bucket as a function of height, measured in pounds.
- Mass of the bucket as a function of height, measured in pounds.
 - Gravitational constant, measured in feet per square second. (
- Gravitational constant, measured in feet per square second. (
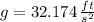 )
)
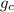 - lb-f to lb-m conversion factor, measured in lb-m to lb-f. (
- lb-f to lb-m conversion factor, measured in lb-m to lb-f. (
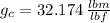 )
)
Since leaking is constant, the mass of the bucket can be modelled by using a first-order polynomial (linear function), that is:

Where:
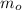 - Initial mass of the bucket, measured in pounds.
- Initial mass of the bucket, measured in pounds.
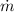 - Leaking rate, measured in pounds per feet.
- Leaking rate, measured in pounds per feet.
 - Height of the bucket with respect to bottom, measured in feet.
- Height of the bucket with respect to bottom, measured in feet.
After replacing the mass and simplifying the integral, the following expression for work is found:


If
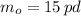 ,
,
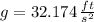 ,
,
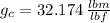 ,
,
 and
and
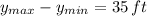 , the work done lifting the bucket to the top of the building is:
, the work done lifting the bucket to the top of the building is:
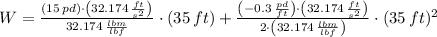
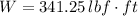
The work done lifting the bucket to the top of the building is 341.25 lbf-ft.