Options
- 0.7+0.2−0.4=0.5
- 0.7+0.2=0.9
- 0.7+0.4=1.1
- 0.4+0.2=0.6
- 0.7+0.4−0.2=0.9
Answer:
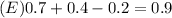
Explanation:
In probability theory
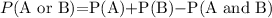
Let the event that the show had animals in it = A
P(A)=0.7
Let the event that the show aired more than 10 times =B
P(B)=0.4
P(A and B)= 0.2
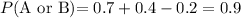
Therefore, the equation which shows the correct use of the addition rule to determine the probability that a randomly selected show had animals in it or aired more than 10 times is:
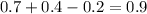
The correct option is E.