Answer:
(D)E(evens) = E(odds) because the different probabilities and values end up balancing out, creating a fair game. Therefore, Jessica may choose whichever she likes.
Explanation:
The table of the probability of rolling the sums is presented below.
![\left\begin{array}{ccccccccccccc}$Roll&2&3&4&5&6&7&8&9&10&11&12\\\\$Prob&(1)/(36)&(2)/(36)&(3)/(36)&(4)/(36)&(5)/(36)&(6)/(36)&(5)/(36)&(4)/(36)&(3)/(36)&(2)/(36)&(1)/(36) \end{array}\right]()
P(an even sum)
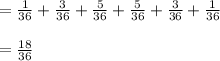
Therefore, P(an odd sum)
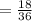
Therefore, E(evens) = E(odds) because the different probabilities and values end up balancing out, creating a fair game. Therefore, Jessica may choose whichever she likes.