ii) When a polynomial f(x) is divided by (x-1) and (x+2) it leaves remainder 5 and 17 respectively. find the remainder when f(x) is divided by (x-1) (x+2)
14) The remainder when the expression ax³ + bx² + 2x + c is divided by x-1
is twice of that when it is divided by x + 1. Show that c = 3a - b + 6.
Answer:
ii) R(x) = -4x + 9
14) c = 3a - b + 6 ( Proved)
Explanation:
14) The correct expression is
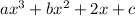
To get the remainder when the expression
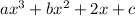 is divided by
is divided by
x - 1, let x - 1 = 0; x = 1
Remainder:
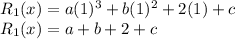
When
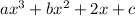 is divided by x + 1
is divided by x + 1
Let x + 1 = 0; x = -1
Remainder:
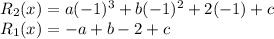
According to the question, R₁(x) = 2R₂(x)
a + b + 2 + c = 2(-a + b - 2 + c)
a + 2a +b - 2b + 2 + 4 = 2c - c
c = 3a - b + 6 ( Proved)
ii)
The dividend is f(x)
(x - 1)(x + 2) is the divisor, i.e. D(x) = (x - 1)(x + 2)
Let the quotient = A(x)
Let the Remainder, R(x) = ax + b..............(1)
Therefore, f(x) = A(x)D(x) + R(x)
f(x) = A(x)(x - 1)(x + 2) + R(x)...................(2)
When f(x) is divided by x - 1, x = 1
Put x = 1 into equation (2) knowing that R(1) = 5
f(1) = R(1) = 5
R(1) = a(1) + b = 5
a + b = 5....................(3)
When f(x) is divided by x + 2, x = -2
Put x = -2 into equation (2) knowing that R(-2) = 17
f(-2) = R(-2) = 17
R(-2) = a(-2) + b = 17
-2a + b = 17..................(4)
Subtracting equation (1) from (2)
-3a = 12
a = -12/3
a = -4
Substitute the value of "a" into equation (4)
-2(-4) + b = 17
8 + b = 17
b = 9
Since R(x) = ax + b
R(x) = -4x + 9