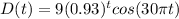Question

A spring is attached to the ceiling and pulled 9 cm down from equilibrium and released. The amplitude decreases by 7% each second. The spring oscillates 15 times each second. Find an equation for the distance, D the end of the spring is below equilibrium in terms of seconds, t.

Answer 1

`D(t) = 9(0.93)^t cos(30 \pi t)`

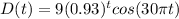
Step-by-step explanation:

Amplitude begins at 9 cm,
`A_0 = 9 cm`

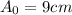
The amplitude decreases by 7% (0.07) each second

The amplitude function can then be modeled as:

`A(t) = A_0(1 - 0.07)^t\\A(t) = 9(0.93)^t`

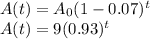
The spring oscillates 15 times each second, the period of oscillation (time to make 1 oscillation) will therefore be calculated as:

T = 1/15

`(2\pi )/(B) = (1)/(15) \\\\B = 30\pi`

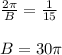
The graphical equation of the system described is:

`D(t) = A cos ( Bt - C) + D`

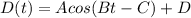
Horizontal shift, C = 0

Vertical shift, D = 0

`D(t) = 9(0.93)^t cos(30 \pi t)`