Question

A plane wave has the equation y=25sin(120t-4x). Find (a) amplitude (b) wave length (c) frequency (d) speed

Answer 1

a) The amplitud of the plain wave is 25, b) The wave length of the plain wave is
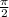`(\pi)/(2)`, c) The frequency of the plain wave is
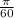`(\pi)/(60)`, d) The speed of propagation of the plain wave is 0.082.

Explanation:

A plain wave is modelled after the following mathematical model as a function of time and horizontal position. That is:

`y(t, x) = A \cdot \sin (\omega\cdot t - (2\pi)/(\lambda)\cdot x)`

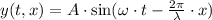
Where:

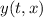`y(t, x)` - Vertical position wave with respect to position of equilibrium, dimensionless.

`A` - Amplitude, dimensionless.

`\omega` - Angular frequency, dimensionless.

`\lambda` - Wave length, dimensionless.

After comparing this expression with the equation described on statement, the following information is obtained:

`A = 25`,
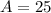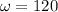`\omega = 120` and
`(2\pi)/(\lambda) = 4`

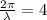
a) The amplitude of the plain wave is 25.

b) The wave length associated with the plain wave is found after some algebraic handling:

`(2\pi)/(\lambda) = 4`

`\lambda = (\pi)/(2)`

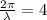
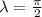
The wave length of the plain wave is
`(\pi)/(2)`.

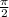c) The frequency can be calculated in term of angular frequency, that is:

`f = (2\pi)/(\omega)`

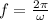
Where
`f` is the frequency of the plain wave.

If
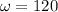`\omega = 120`, then:

`f = (2\pi)/(120)`

`f = (\pi)/(60)`

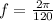
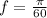
The frequency of the plain wave is
`(\pi)/(60)`.

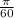d) The speed of propagation is equal to the product of wave length and frequency:

`v = \lambda \cdot f`

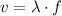
Given that
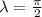`\lambda = (\pi)/(2)` and
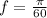`f = (\pi)/(60)`, the speed of propagation is:

`v = \left((\pi)/(2) \right)\cdot \left((\pi)/(60) \right)`

`v \approx 0.082`

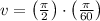
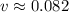
The speed of propagation of the plain wave is 0.082.