Question

A car is known to be 88% likely to pass inspection at a certain Motor Vehicle Agency inspection office. What is the probability that at least 90 cars pass inspection if a random sample of 100 cars is taken at this Motor Vehicle Agency inspection office? A. 0.4032 B. 0.6663 C. 0.3337 D. 0.88

Answer 1

The correct option is;

C. 0.3337

Explanation:

We note that for a binomial probability distribution, we have;

`p(r\geq \gamma)=\sum_(\gamma = r)^( n)\dbinom{n}{r}\cdot \left (p\right )^(\gamma )\cdot \left (1-p\right )^(n - \gamma)`

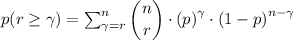
Which gives;

`p(x \geq 90)=\sum_(r = 90)^( 100)\dbinom{100}{90}\cdot \left (0.88\right )^(\gamma )\cdot \left (1-0.88\right )^(100 - \gamma)`

`\dbinom{100}{90}\cdot \left (0.88\right )^(90 )\cdot \left (1-0.88\right )^(10) = 0.108033`

`\dbinom{100}{91}\cdot \left (0.88\right )^(91 )\cdot \left (1-0.88\right )^(9) = 0.08706`

`\dbinom{100}{92}\cdot \left (0.88\right )^(92 )\cdot \left (1-0.88\right )^(8) = 0.062456`

`\dbinom{100}{93}\cdot \left (0.88\right )^(93 )\cdot \left (1-0.88\right )^(7) = 0.039399`

`\dbinom{100}{94}\cdot \left (0.88\right )^(94 )\cdot \left (1-0.88\right )^(6) = 0.021516`

`\dbinom{100}{95}\cdot \left (0.88\right )^(95 )\cdot \left (1-0.88\right )^(5) = 0.09965`

`\dbinom{100}{96}\cdot \left (0.88\right )^(96 )\cdot \left (1-0.88\right )^(4) = 0.003806`

`\dbinom{100}{97}\cdot \left (0.88\right )^(97 )\cdot \left (1-0.88\right )^(3) = 0.001151`

`\dbinom{100}{98}\cdot \left (0.88\right )^(98 )\cdot \left (1-0.88\right )^(2) = 0.000258`

`\dbinom{100}{99}\cdot \left (0.88\right )^(99 )\cdot \left (1-0.88\right ) = 0.0000383`

`\dbinom{100}{100}\cdot \left (0.88\right )^(100 )\cdot \left (1-0.88\right )^(0) = 0.00000281`

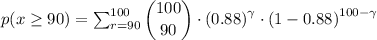
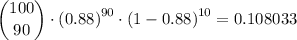
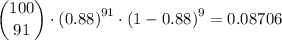
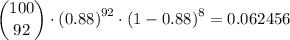
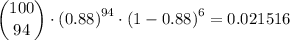
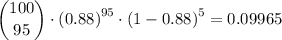
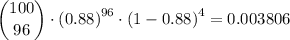
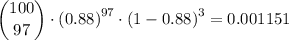
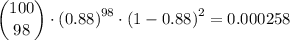
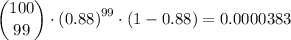
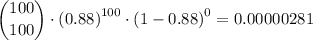
P(r≥90) is therefore 0.1083 + 0.08706 + 0.062456 + 0.039399 + 0.021516 + 0.09965 + 0.003806 + 0.001151 + 0.000258 + 0.0000383 + 0.00000281 = 0.333685 ≈ 0.3337.