Answer and Step-by-step explanation:
Since it is given that
AB || DC
BC || AE
Based on this we can conclude that
If AB || DC
So we can say
∠ABE ≅ ∠CDB
This indicates that the alternate interior angles are congruent i.e its angle and sides are equal
Now
If BC || AE
So we can say
∠CBD ≅ ∠BEA
This indicates that the alternate interior angles are congruent i.e its angle and sides are equal
Now
ΔAEB is same as ΔCBD
This indicates that in one triangle two angles are same to another two angles so both triangles are similar to each other i.e this is a AA Similarity Postulate
Finally we proof
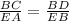
As the same sides are proportional to each other
We compared both based on interior angles