Question

Find the perimeter of the rhombus below, given that a=9 and b=15. Round your answer to one decimal place, if necessary.

Answer 1

Answer: 35.0 units long.

Explanation:

You can treat a rhombus as four right triangles, where there is a short side, a long side, and a hypotenuse.

The hypotenuse of a right triangle inside a rhombus will always be on the exterior.

To find the hypotenuse of one of the right triangles, use the Pythagorean theorem:

`a^2 + b^2 = c^2`

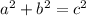
We are given that a = 9 and b = 15, but in order to get the values needed for the theorem, we must divide them by 2 in order to get the sides for the triangles.

9 / 2 = 4.5, 15 / 2 = 7.5

Then, you can substitute your values into the Pythagorean theorem:

`4.5^2 + 7.5^2 = c^2\\\\20.25 + 56.25 = 76.5\\\\c^2 = 76.5\\c = 8.7464`

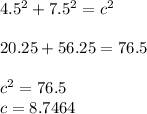
Knowing that one of the external sides is 8.7464 units long, you can then multiply that value by 4 to get your perimeter, as there are four identical sides forming the perimeter:

8.7464 * 4 = 34.9856. Rounded: 35.0