Question

*ANSWER ASAP , 0SEE ATTACHMENTS BELOW* What is the area of the polygon?

Answer 1

14 sqr units

Explanation:

divide the polygon into two triangle

the area of a triangle H = 1/2 *2 *7 = 7

so the area of the polygon = 2*H = 14

Answer 2

14 units

Solution,

A( 1,4)

B(3,6)

C(8,4)

D(3,2)

Now,

Finding the distance of A and C

A(1,4)----->(X1, y1)

C (8,4)---->(x2, y2)

AC :

√(x2,X1)^2+ (y2-y1)^2

`\sqrt{ {(8 - 1)}^(2) + {(4 - 4)}^(2) }`

`\sqrt{ {(7)}^(2) + {(0)}^(2) }`

`√(49)`

`\sqrt{ {(7)}^(2) }`

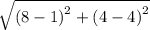
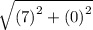
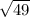
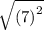
7 units

AC = 7 units

By connecting BD, we get 2 triangles

i.e ∆ABD and ∆ BCD

Total area of polygon

= Area of ∆ ABD + Area of ∆ BCD

Area of ∆ABD

= 1/2 * base *height

= 1/2* BD * AO

= 1/2*4*2

= 4 units

Again,

Area of ∆BCD

= 1/2* base* height

= 1/2 * BD*CO

= 1/2*4*5

= 10 units

Total area:

= Area of ∆ ABD + Area of ∆ BCD

= 4 units +10 units

= 14 units

Hope this helps...

Good luck on your assignment..