Question

It's 11 that grade, please help me I'm stuck ​

Answer 1

Limit
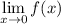`$\lim_(x \to 0) f(x)$` does not exist.

Explanation:

To calculate left hand limit, we use a value slightly lesser than that of 0.

To calculate right hand limit, we use a value slightly greater than that of 0.

Let h be a very small value.

Left hand limit will be calculate at 0-h

Right hand limit will be calculate at 0+h

First of all, let us have a look at the value of f(0-h) and f(0+h)

`f(0-h)=f(-h) = (-h)/(|-h|)\\\Rightarrow (-h)/(h) = -1`

`f(0-h)=-1 ....... (1)`

`f(0+h)=f(h) = (h)/(|h|)\\\Rightarrow (h)/(h) = 1`

`f(0+h)=1 ....... (2)`

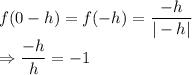
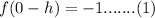
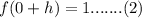
Now, left hand limit:

`$\lim_(x \to 0^(-) ) f(x)$\\` =
`$\lim_(h \to 0) f(0-h)$`

`\Rightarrow`
`$\lim_(h \to 0) f(-h)$`

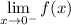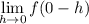
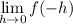
Using equation (1):

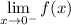`$\lim_(x \to 0^(-) ) f(x)$\\` = -1

Now, Right hand limit:

`$\lim_(x \to 0^(+) ) f(x)$\\` =
`$\lim_(h \to 0) f(0+h)$`

`\Rightarrow`
`$\lim_(h \to 0) f(h)$`

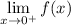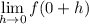
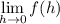
Using equation (2):

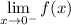`$\lim_(x \to 0^(-) ) f(x)$\\` = 1

Since Left Hand Limit
`\\eq` Right Hand Limit

So, the answer is:

Limit
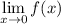`$\lim_(x \to 0) f(x)$` does not exist.