Answer:
(a)
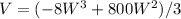
(b)

Explanation:
Let's call the length of the box L, the width W and the height H. Then, we can write the following equations:
"A rectangular box has a base that is 4 times as long as it is wide"
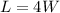
"The sum of the height and the girth of the box is 200 feet"
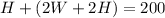
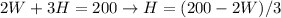
The volume of the box is given by:

Using the L and H values from the equations above, we have:
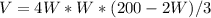
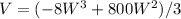
The domain of V(W) is all positive values of W that gives a positive value for the volume (because a negative value for the volume or for the width doesn't make sense).
So to find where V(W) > 0, let's find first when V(W) = 0:
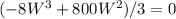
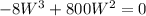
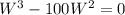

The volume is zero when W = 0 or W = 100.
For positive values of W ≤ 100, the term W^2 is positive, but the term (W - 100) is negative, then we would have a negative volume.
For positive values of W > 100, both terms W^2 and (W - 100) would be positive, giving a positive volume.
So the domain of V(W) is W > 100.