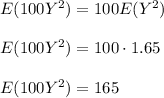The question is incomplete! Complete question along with answer and step by step explanation is provided below.
Question:
An individual who has automobile insurance from a certain company is randomly selected. Let Y be the number of moving violations for which the individual was cited during the last 3 years. The pmf of Y is:
y | P(Y)
0 | 0.50
1 | 0.20
2 | 0.25
3 | 0.05
Compute E(Y)
Suppose an individual with Y violations incurs a surcharge of $100Y2. Calculate the expected amount of the surcharge.
Answer:
The expected value E(Y) is
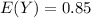
The expected amount of the surcharge is
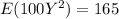
Explanation:
Let Y be the number of moving violations for which the individual was cited during the last 3 years.
The given probability mass function (pmf) of Y is
y | P(Y)
0 | 0.50
1 | 0.20
2 | 0.25
3 | 0.05
Compute E(Y)
The expected value E(Y) is given by
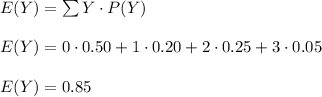
Suppose an individual with Y violations incurs a surcharge of $100Y2. Calculate the expected amount of the surcharge.
The expected amount of the surcharge is given by
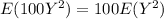
Where
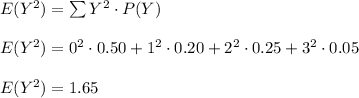
So, the expected amount of the surcharge is