Question

negative binomial rv is the number of failures that occur before the rth success in a sequence of independent and identical success/failure trials. The probability mass function (pmf) of X is

Answer 1

The probability mass function (pmf) of X is:

`P(X=k)={{k+r-1}\choose k}\cdot (1-p)^(k)\cdot p^(r);\ k=1,2,3,...`

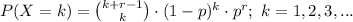
Explanation:

The random variable X is said to be a Negative Binomial random variable.

The random variable X is defined as the number of failures in a series independent and identical Bernoulli trials, before a specific number of success takes place.

For example, consider rolling a 5 on a six-sided die as the success and any other number as failure. Then the number of rolls before 5 occurs three times in a row can be defined as a negative binomial experiment.

The probability mass function of a negative binomial random variable X is:

`P(X=k)={{k+r-1}\choose k}\cdot (1-p)^(k)\cdot p^(r);\ k=1,2,3,...`

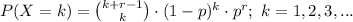
Here,

k = number of successes

r = number of failures

p = probability of success