Question

Determine whether the lines L1:x=25+7t,y=17+6t,z=t and L2:x=−12+8ty=−17+8tz=−11+4t intersect, are skew, or are parallel. If they intersect, determine

Answer 1

Answer: The lines are skew.

Explanation: Two lines can only be parallel OR skew Or intersect each other. To determine that:

1) If the lines are parallel, divide the coefficient that precedes the variable of each equation and compare:

`(7)/(8) \\eq (6)/(8) \\eq (1)/(4)`

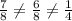
Since they are not equal, L1 and L2 are not parallel.

2) If the lines intersect, when you equal the equations the variable is a valid statement:

25 + 7t = - 12 + 8t (1)

17 + 6t = - 17 + 8t (2)

t = - 11 + 4t (3)

Using (3) to solve the system:

t - 4t = - 11

3t = 11

t =
`(11)/(3)`

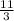
Substituing t in (1):

25 + 7(11/3) = -12 + 8(11/3)

25 + 77/3 = - 12 + 88/3

`(152)/(3) = (52)/(3)`

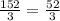
Which is not true, so, the lines does NOT intersect.

As they are none of the other options, it can be concluded that the lines L1 and L2 are skew.