Question

A standard six-sided die is rolled $6$ times. You are told that among the rolls, there was one $1,$ two $2$'s, and three $3$'s. How many possible sequences of rolls could there have been? (For example, $3,2,3,1,3,2$ is one possible sequence.)

Answer 1

`Sequence = 120`

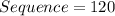
Explanation:

Given

6 rolls of a die;

Required

Determine the possible sequence of rolls

From the question, we understand that there were three possible outcomes when the die was rolled;

The outcomes are either of the following faces: 1, 2 and 3

Total Number of rolls = 6

Possible number of outcomes = 3

The possible sequence of rolls is then calculated by dividing the factorial of the above parameters as follows;

`Sequence = (6!)/(3!)`

`Sequence = (6 * 5 * 4* 3!)/(3!)`

`Sequence = 6 * 5 * 4`

`Sequence = 120`

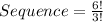
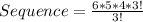
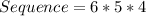
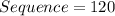
Hence, there are 120 possible sequence.