Question

A student on a skateboard is moving at a speed of 1.40 m/s at the start of a 2.15 m high and 12.4 m long incline. The total mass is 53.0 kg, air resistance and rolling resistance can be modeled as a constant friction force of 41.0 N, and the speed at the lower end of the incline is 6.90 m/s. Determine the work done (in J) by the student as the skateboard travels down the incline. -415.39 Incorrect: Your answer is incorrect.

Answer 1

W = 609.97J

Step-by-step explanation:

In order to calculate the work done by the student, you take into account that the total work is equal to the change of the kinetic energy of the student, as follow:

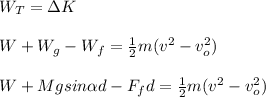`W_T=\Delta K\\\\W+W_g-W_f=(1)/(2)m(v^2-v_o^2)\\\\W+Mgsin\alpha d-F_fd=(1)/(2)m(v^2-v_o^2)` (1)

The work done by the friction force is negative because it is against the motion of the student.

W: work done by the student = ?

Wf: work done by the friction force

Wg: work done by the gravitational force

Ff: total friction force = 41.0N

m: mass of the skateboard = 53.0kg

d: distance traveled by the student

v: final speed of the student = 6.90m/s

vo: initial speed of the student = 1.40m/s

α: angle of the incline

You first calculate the distance d, with the Pythagoras' theorem

`d=√((2.15m)^2+(12.4m)^2)=12.58m`

Furthermore, the angle α is:

`\alpha=tan^(-1)((2.15m)/(12.4m))=9.83\°`

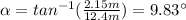
Then, you solve the equation (1) for W and replace the values of all parameters:

`W=(1)/(2)m(v^2-v_o^2)+F_fd-Mgsin\alpha d\\\\W=(1)/(2)(53.0kg)((6.90m/s)^2-(1.40m/s)^2)+(41.0N)(12.58m)\\-(53.0kg)(9.8m/s^2)sin(9.83\°)(12.58m)\\\\W=609.97J`

The work done by the student is 609.97J