Question

The accompanying data represent the miles per gallon of a random sample of cars with a​ three-cylinder, 1.0 liter engine.

31.5 36.0 37.8 38.5 40.1 42.234.2 36.2 38.1 38.7 40.6 42.534.7 37.3 38.2 39.5 41.4 43.435.6 37.6 38.4 39.6 41.7 49.3

​(a) Compute the​ z-score corresponding to the individual who obtained 32.3 miles per gallon. Interpret this result. ​(b) Determine the quartiles. ​(c) Compute and interpret the interquartile​ range, IQR. (d) Determine the lower and upper fences. Are there any​ outliers?

Answer 1

Explained below.

Explanation:

The data provided is as follows:

S = {31.5, 36.0, 37.8, 38.5, 40.1, 42.2, 34.2, 36.2, 38.1, 38.7, 40.6, 42.5, 34.7. 37.3, 38.2, 39.5, 41.4, 43.4, 35.6, 37.6, 38.4, 39.6, 41.7, 49.3}

Compute the mean and standard deviation as follows:

`\mu=(1)/(n)\sum X=(1)/(24)* [31.5+36.0+37.8+...+49.3]=38.88\\\\\sigma=\sqrt{(1)/(n-1)\sum (X-\mu)^(2)}=\sqrt{(1)/(24-1)* 299.639584}=3.61`

(a)

Compute the​ z-score corresponding to the individual who obtained 32.3 miles per gallon as follows:

`z=(X-\mu)/(\sigma)`

`=(32.3-38.88)/(3.61)\\\\=-1.823`

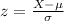
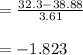
Thus, the z-score corresponding to the individual who obtained 32.3 miles per gallon is -1.823.

(b)

The data set arranged in ascending order is:

S = {31.5 , 34.2 , 34.7 , 35.6 , 36 .0, 36.2 , 37.3 , 37.6 , 37.8 , 38.1 , 38.2 , 38.4 , 38.5 , 38.7 , 39.5 , 39.6 , 40.1 , 40.6 , 41.4 , 41.7 , 42.2 , 42.5 , 43.4 , 49.3}

The set consists of 24 values.

The first and third quartile are:

`Q_(1)=[(n+1)/(4)]^(th)\ obs.=[(24+1)/(4)]^(th)\ obs.=12.5^(th)\ obs.=(36.2+ 37.3)/(2)=36.75\\\\Q_(3)=[(3(n+1))/(4)]^(th)\ obs.=[(3(24+1))/(4)]^(th)\ obs.=18.75^(th)\ obs.=(40.6+41.4)/(2)=41`

Thus, the value of Q₁ is 36.75 and Q₃ = 41.

(c)

Compute the inter-quartile​ range as follows:

`IQR=Q_(3)-Q_(1)=41-36.75=4.25`

The inter-quartile range is 4.25.

The inter-quartile range is the amount of data that is contained within the middle 50% of a set of observations, when arranged in order. It is the distance between the first and third quartile.

(d)

Compute the values of lower and upper fences as follows:

`\text{Lower fence}=Q_(1)-1.5* IQR=36.75-(1.5* 4.25)=30.375\approx 30.38\\\\\text{Upper fence}=Q_(3)+1.5* IQR=41+(1.5* 4.25)=47.375\approx 47.38`

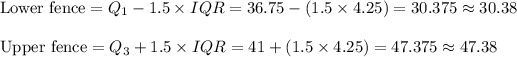
Any values that are less than the lower fence or more than the upper fence are considered as outlier.

Consider the arranged data set.

Only one value is more than the upper fence, 47.38, i.e. 49.3.

So, yes there is one outlier, i.e. 49.3.