Answer:
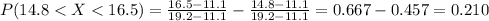
The probability that it will require between 14.8 and 16.5 minutes to perform the task is 0.210
Explanation:
Let X the random variable "completion times for a job task" , and we know that the distribution for X is given by:
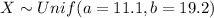
And for this case we wantto find the following probability:
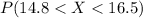
And for this case we can use the cumulative distribution given by:
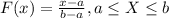
And using this formula we got:
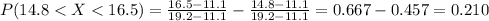
The probability that it will require between 14.8 and 16.5 minutes to perform the task is 0.210