Question

A simple random sample of size nequals200 drivers were asked if they drive a car manufactured in a certain country. Of the 200 drivers​ surveyed, 106 responded that they did. Determine if more than half of all drivers drive a car made in this country at the alpha equals 0.05 level of significance. Complete parts ​(a) through ​(d). ​(a) Determine the null and alternative hypotheses. Upper H 0​: ▼ sigma mu p ▼ not equals less than equals greater than 0.5 Upper H 1​: ▼ p mu sigma ▼ less than greater than not equals equals 0.5 ​(b) Calculate the​ P-value. ​P-valueequals nothing ​(Round to three decimal places as​ needed.) ​(c) State the conclusion for the test. Choose the correct answer below. A. Do not reject Upper H 0 because the​ P-value is greater than the alphaequals0.05 level of significance. B. Do not reject Upper H 0 because the​ P-value is less than the alphaequals0.05 level of significance. C. Reject Upper H 0 because the​ P-value is less than the alphaequals0.05 level of significance. D. Reject Upper H 0 because the​ P-value is greater than the alphaequals0.05 level of significance. ​(d) State the conclusion in context of the problem. There ▼ is not is sufficient evidence at the alpha equals 0.05 level of significance to conclude that more than half of all drivers drive a car made in this country. Click to select your answer(s).

Answer 1

Explained below.

Explanation:

The information provided is:

n = 200

X = 106

α = 0.05

The sample proportion is:

`\hat p=(X)/(n)=(106)/(200)=0.53`

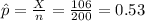
(a)

A hypothesis test is to performed to determine whether more than half of all drivers drive a car made in this country.

The hypothesis is:

H₀: The proportion of drivers driving a car made in this country is less than or equal to 50%, i.e.
`\mu_(p)\leq 0.50`

Hₐ: The proportion of drivers driving a car made in this country is more than 50%, i.e.
`\mu_(p)> 0.50`

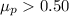
(b)

Compute the value of the test statistic:

`Z=\frac{\hat p-\mu_(p)}{\sqrt{(\mu_(p)(1-\mu_(p)))/(n)}}`

`=\frac{0.53-050}{\sqrt{(0.50(1-0.50))/(200)}}\\\\=0.8485\\\\\approx 0.85`

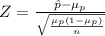
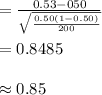
Compute the p-value as follows:

`p-value=P(Z_(0.05)>0.85)\\=1-P(Z_(0.05)<0.85)\\=1-0.80234\\=0.19766\\\approx 0.198`

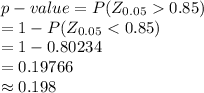
*Use a z-table.

Thus, the p-value of the test is 0.198.

(c)

Decision rule:

Reject the null hypothesis if the p-value is less than the significance level.

p-value = 0.198 > α = 0.05

The null hypothesis will not be rejected.

The correct option is (A).

(d)

Conclusion:

There is not enough evidence at 0.05 level of significance to support the claim that the proportion of drivers driving a car made in this country is more than 50%.