Answer:
Height of the first projectile = 49.98 m
Height of the second projectile = 72.52 m
Step-by-step explanation:
From the given information;
Two projectiles are thrown from the same point with the velocity of49m/s
First is projected making an angle θ with the horizontal
and the second at an angle of 90 - θ.
Thus; for the first height to the horizontal; we have;
 ----- (1)
----- (1)
the second height in the vertical direction is :
 -----(2)
-----(2)
However; the second is found to rise 22.5 m higher than the first; so , we have :
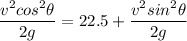
Let's recall that :
Cos²θ = 1 - Sin²θ
Replacing it into above equation; we have:
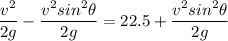
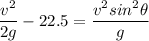
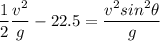
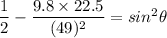
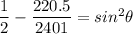
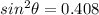
From (1);

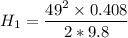
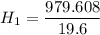
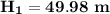
Height of the first projectile = 49.98 m
Similarly;
From(2)


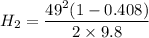
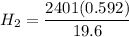

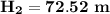
Height of the second projectile = 72.52 m