Question

An incompressible Newtonian fluid is brought to flow in a pipe by pulling a wire in the center at a velocity of 18 cm/s. The wire has a diameter of 5 cm, while the stationary pipe has a diameter of 10 cm. Calculate the shear stress(tre) in the fluid using Newtonian's law of viscosity. The flow is isothermal at °25 and the fluid has a viscosity of 3.0 cp. Provide the sketch of the velocity profile.

Answer 1

The shear stress is 2.16 Pa

Step-by-step explanation:

Newton's law of viscosity can be expressed as follows;

`\tau =\mu * (dv)/(dy)`

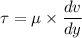
Where:

τ = Shear stress in the fluid

Given that the diameter of the wire = 5 cm

The velocity of the wire = 18 cm/s

The diameter of the pipe = 10 cm

The fluid viscosity, μ = 3.0 cp = 1×10⁻³· Pa·s

The change in velocity from the surface of the wire to the internal surface of the pipe = dv = 18 cm/s

The change in the y (perpendicular) direction of motion of the fluid from the surface of the wire to the interior surface of the tube = dy = 10/2 - 5/2 = 2.5 cm

By putting in the values, we have;

`\tau =0.3 * (18)/(2.5) = 2.16 \ Pa`

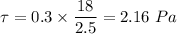
The shear stress = 2.16 Pa