Answer:
The area of polygon MNOPQR = Area of a rectangle that is 15 square units + Area of a rectangle that is 2 square units.
Explanation:
We are given that a polygon MNOPQR is shown. The top vertex on the left is labeled M, and the rest of the vertices are labeled clockwise starting from the top-left vertex labeled, M. The side MN is parallel to side QR. The side MR is parallel to side PQ.
The side MN is labeled as 5 units. The side QR is labeled as 7 units. The side MR is labeled as 3 units, and the side NO is labeled as 2 units.
Firstly, we will draw a perpendicular line from point O which meets the line RQ at point T. Now, the polygon MNOPQR is divided into two rectangles MNTR and OPQT.
As we know that the area of the rectangle =
In the rectangle MNTR, the length (MN) = 5 units and the breadth (MR) = 3 units.
So, the area of the rectangle MNTR =
=
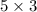= 15 square units
Now, as we know that in rectangle MNTR, the side NT = 3 units and the side NO is labeled as 2 units. This means that the side OT = NT - NO = 3 units - 2 units = 1 unit
Similarly, the side QR is labeled as 7 units and the side RT is labeled as 5 units. This means that the side TQ = QR - RT = 7 - 5 = 2 units
Now, in the rectangle OPQT, the length (TQ) = 2 unit and the breadth (OT) = 2 units.
So, the area of the rectangle OPTQ =
=
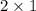= 2 square units
Hence, the area of polygon MNOPQR = Area of a rectangle that is 15 square units + Area of a rectangle that is _2_ square units.