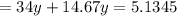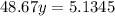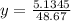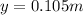Question

Two long, parallel, current-carrying wires lie in an xy-plane. The first wire lies on the line y = 0.350 m and carries a current of 34.0 A in the +x direction. The second wire lies along the x-axis. The wires exert attractive forces on each other, and the force per unit length on each wire is 285 µN/m. What is the y-value (in m) of the line in the xy-plane where the total magnetic field is zero?

Answer 1

y = 0.105 m

Explanation:

Given:

First wire: y = 0.350m & Current, I = 34.0A

Force per unit length on each wire = 285 µN/m

Required:

What is the y-value (in m) of the line in the xy-plane where the total magnetic field is zero?

First find the current in the second wire:

`(u_0 I_1 I_2)/(2\pi d) = 285*10^-^6`

`(2*10^-^7 * 34 * I_2)/(0.35) = 285 * 10^-^6`

`I_2 = (285*10^-^6 * 0.35)/(2*10^-^7 * 34) = 14.67`

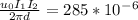
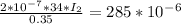
Current in wire 2 = 14.67 A

Let y distance have zero magnetic field

Take the formula:

`(u_0 I_2)/(2\pi y) = (u_0 I_1)/(2\pi(0.35 - y))`

`= (2*10^-^7 * 14.67)/(2\pi y) = (2*10^-^7 * 34)/(2\pi(0.35 - y))`

[

`= 14.67 * (0.35 - y) = 34y`

`= 5.1345 - 14.67y = 34y`

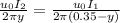
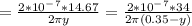
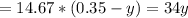
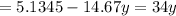
Collect like terms

`= 34y + 14.67y = 5.1345`

`48.67y = 5.1345`

`y = (5.1345)/(48.67)`

`y = 0.105 m`