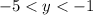Full Question:
The function
![y =\sqrt[3]{-x} - 3](https://img.qammunity.org/2021/formulas/mathematics/college/k44mcqkuvupcximkdw2o6571akjheczo2i.png) is graphed only over the domain of –8 < x < 8. what is the range of the graph?
is graphed only over the domain of –8 < x < 8. what is the range of the graph?
Answer:
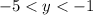
Explanation:
Given
Function:
![y =\sqrt[3]{-x} - 3](https://img.qammunity.org/2021/formulas/mathematics/college/k44mcqkuvupcximkdw2o6571akjheczo2i.png)
Range: x
Required
Find the range of the graph
To calculate the range of the graph; we simply substitute the value of x (the domain) at both ends to the given function;
In other words, solve for y when x = -8 and when x = 8
To start with;
When x = -8
![y =\sqrt[3]{-x} - 3](https://img.qammunity.org/2021/formulas/mathematics/college/k44mcqkuvupcximkdw2o6571akjheczo2i.png)
![y =\sqrt[3]{-(-8)} - 3}](https://img.qammunity.org/2021/formulas/mathematics/college/i4eqak25lennmyyj3rvlvcjsh4o41b8rn2.png)
![y =\sqrt[3]{8} - 3}](https://img.qammunity.org/2021/formulas/mathematics/college/j2059gyqjbx6o80m2nyhjwm3pvxysj6m0b.png)

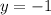
When x = 8
![y =\sqrt[3]{-8} - 3](https://img.qammunity.org/2021/formulas/mathematics/college/bmehdhkbqybemdktq09s9hq1upekcp19uj.png)
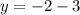
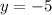
Converting both values of y to inequalities
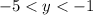
Hence, the range of the graph is